Functions in mathematics

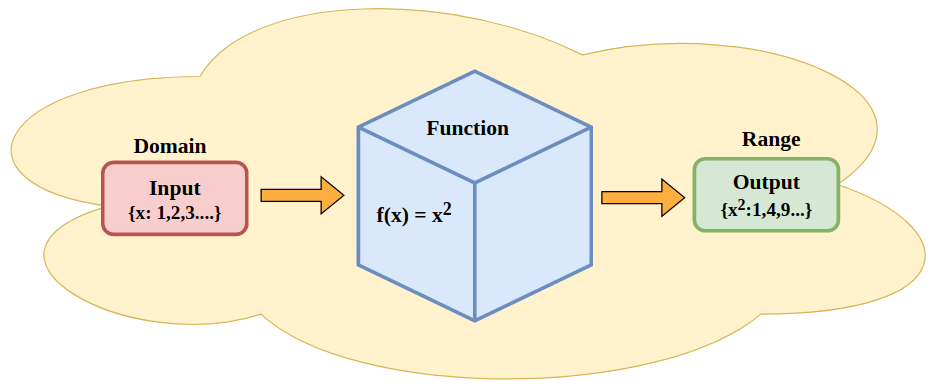
Although the concept of function is applicable in many fields, we might be accustomed to find it in mathematics.

Intuitively, a function is a binary relation between two sets. If we denote the sets by \(X\) and \(Y\), and the function that relates them by \(f\), it is customary to denote the relation as

\begin{equation*} f \colon X \to Y. \end{equation*}

When the sets \(X\) and \(Y\) are subsets of numerical sets (e.g. natural \(\mathbb{N}\), integers \(\mathbb{Z}\), real \(\mathbb{R}\) or complex \(\mathbb{C}\) numbers), functions that relate them might be called numerical functions.

Numerical functions as transformation

Hey son! Santiago is one hundred kilometers away. If we drive at one hundred kilometers per hour, How long would it take us to get there?

One hour dad.

Yes, you're right. If we travel to Valdivia, that is one thousand kilometers away, How many hours would we be traveling?

Hmm… Let me think… Ten hours.

The above situation describes the use of a function, in fact a numerical function, to model a physical system (distance traveled by a vehicle). Mathematically, our function is denoted as

\begin{equation*} f(t) = 100 t. \end{equation*}

Above, we are assuming that the time is measured in hours and the traveled distance, \(f(t)\), is measured in kilometers per hour.

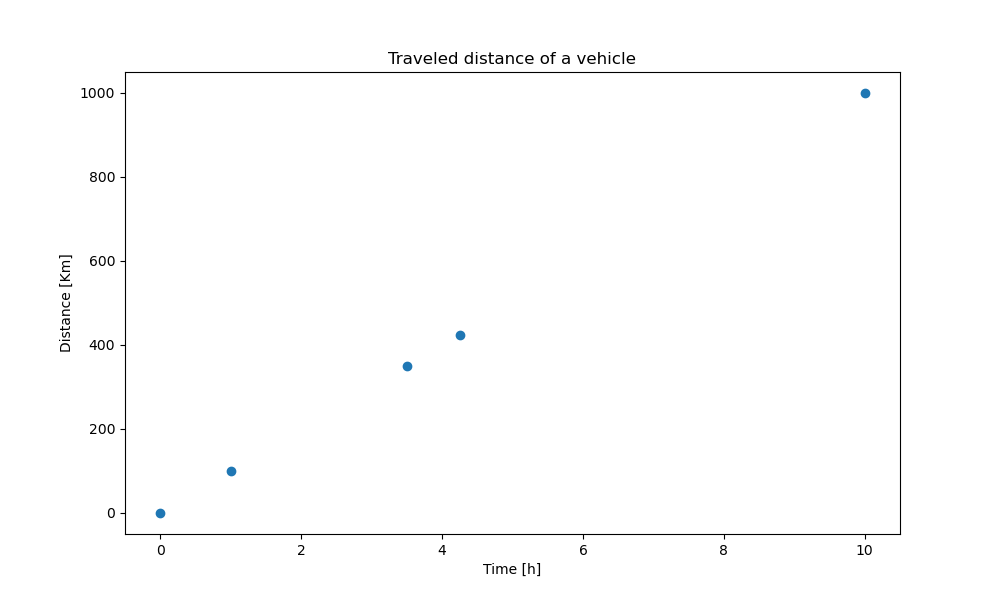
Let's use python to build a relational table a set of values of time. For that we select different values of time, e.g. \(t = \left\{ 0, 1, 3.5, 4.25, 10 \right\}\), and then use the transformation rule to compute the traveled distance.

times = [0, 1, 3.5, 4.25, 10]
distances = []
for time in times:
    distances.append(100 * time)

return times, distances

0	1	3.5	4.25	10
0	100	350.0	425.0	1000

Note that the results can be beautifully summarized in a table, a two-dimensional array of numerical values. This is data. In fact, we are considering a discrete subset of a continuous data.

We can plot our data:

import matplotlib.pyplot as plt
times = [0, 1, 3.5, 4.25, 10]
distances = []
for time in times:
    distances.append(100 * time)

plt.figure(figsize=(10,6))    
plt.scatter(times, distances)
plt.xlabel("Time [h]")
plt.ylabel("Distance [Km]")
plt.title("Traveled distance of a vehicle")
plt.savefig(filename)
return filename

Importance of numerical functions

Numerical functions are fundamental when we try to build a model for predicting the behavior of a system, as in the previous section. In computer science, a neuron (the basic structure behind artificial intelligence) is a very simple numerical function.